Fisheye lens

A fisheye lens is a lens with a viewing angle close to or equal to 180° (maybe greater than 180°). It is an extreme wide-angle lens, fisheye lens is its common name. In order to maximize the viewing angle of the lens, the front lens of this photographic lens has a short diameter and a parabolic projection to the front of the lens, which is quite similar to the eyes of a fish, so it is called a fisheye lens.

The shorter the focal length, the larger the viewing angle, and the stronger the distortion due to optical principles. In order to achieve or exceed the super-large viewing angle of 180 degrees, the designer of the fisheye lens has to make sacrifices to allow this kind of distortion to exist reasonably. As a result, except for the scene in the center of the picture, the other scenes that should have been horizontal or vertical have changed accordingly.

A fisheye lens is an optical imaging system with a large field of view and a large aperture. Generally, two or three negative meniscus lenses are used as the front lens group to compress the object-side large field of view to the field of view required by a conventional lens. For object point imaging with a large field of view, the beam hits the optical surface of the front lens group at a larger incident angle. After imaging by the optical system, the focus position in the meridian and sagittal planes may be completely inconsistent with the wavefront parameters. The exit angle is small. Therefore, a fisheye lens has the imaging characteristics of a plane symmetric optical system, but the aberration analysis of an axisymmetric optical system is not suitable for this.

Security cameras generally also use fisheye lenses. The imaging principle of fisheye lenses is different from that of ordinary lenses. It is not a one-time imaging. At the same time, the focal length is different from ordinary lenses, and the focal length of the fisheye lens will not affect the viewing distance and viewing angle. Nevertheless, the focal length of fisheye lenses used in security cameras is generally small. On the other hand, a fisheye lens camera cannot see too far, and is generally suitable for installation in a relatively narrow and enclosed space, such as the middle of the hall, the elevator, and the middle of the room.

Fisheye lens type

Fisheye lenses can be divided into round fisheye lenses and full-frame fisheye lenses due to the different image effects they present.

• Round fisheye lens. The circular fisheye lens has a vertical viewing angle of 180°, and the horizontal and diagonal viewing angles are also 180°. The image sensor (sensor) is generally rectangular. According to the design, the image range covered by most round fisheye lenses is smaller than that of linear lenses. Therefore, the corners around the picture taken by the round fisheye lens with the rectangular sensor are completely black.
• Full frame fisheye lens. The fisheye lens enlarges the image circle to cover the entire sensor rectangular frame, which is called a “full-frame fisheye lens”. The diagonal viewing angle of the picture taken by this fisheye lens is 180°, and the horizontal and vertical viewing angles are both less than 180°.

In the security field, the camera that uses a round fisheye lens is generally called a 360-degree panoramic fisheye camera, and the one that uses a full-frame fisheye lens is called a 180-degree panoramic camera. It should be noted that whether it is a so-called 360-degree circular image or a 180-degree rectangular image, through the back-end software and algorithm correction processing, the corresponding back-end (mobile app, NVR or management software) can show different Image effects.

Lens angle

As mentioned earlier, the angle of view of the fisheye lens is not determined by the focal length, but is calculated and designed according to different projection mapping methods. Generally, the angle of view of a fisheye lens is designed to be 180°, of course, there are also 190°, 200°, etc. The largest fisheye lens on the market currently has a viewing angle of 280°. Considering the cost, design process and other optical alternatives, a fisheye lens with a larger viewing angle does not have much practical significance.

As described in the article “Lens of security camera”, the size of the target surface of the fisheye lens is best to be the same as that of the sensor, so that the best image effect can be obtained. The following figure shows several different matching effects of the lens and the sensor target surface.

Lens projection mapping method

Assuming that the angle between a certain point in the field of view and the optical axis is θ, and the distance from the center of the film formed by this point on the sensor is r, then, for an ordinary lens, r = f × tan(θ), where f is focal length. Since the size of the sensor is fixed, that is, the maximum value of r is fixed, so the maximum value of θ corresponds to the focal length f. The shorter the f, the larger the maximum value of θ, that is, the wider the field of view.

However, fisheye lenses do not follow this linear projection relationship. There are four common projection methods for fisheye lenses:

Orthographic, orthogonal projection. This projection method is like slapping the entire hemisphere directly, and the formula is r=fsin⁡(θ). Among several projection methods, this projection method brings the most distortion and compresses the edge objects the most, and the compression of the central image is relatively low, so it is rarely used in practice. Obviously, the maximum angle of view of this projection method cannot be greater than 180°.

Equisolid angle, equal solid angle projection, azimuth equal area projection. This projection method can maintain the surface relationship. Using the formula to express the relationship between the distance r from the center of the image and the incident angle θ is r=2fsin⁡(θ/2). Each pixel has an equal solid angle or an equal area on the unit sphere. Looks like a mirror image on a ball, with the best special effects (precise distance), suitable for area comparison (such as determining the degree of cloud in the sky). This kind of projection method is widely used, it will compress the edge objects, and the cost is very high.

Equidistant, isometric projection, azimuth isometric projection. The characteristic of this projection method is that the distance of the object from the center of the image on the imaging surface is proportional to the angle of the object from the optical axis in space, and this proportionality factor is the focal length of the lens. The formula to express the relationship between this distance and angle is r=fθ. Under this projection transformation, the distance (angle) of the object from the center is an important geometric property, and the spatial angular distance of the object is proportional to the planar distance of the image of the object on the image plane. This is also the source of the name of this projection method. This method of lens is more used in the military field. Imagine a weapon aiming system. Using this kind of projection lens not only monitors a large field of view, but also for the azimuth angle of the target, it is only necessary to directly measure the plane distance in the screen, which is very convenient. In the simulation scenario in the figure below, the height of each small square in the middle column is the same.

Stereographic, stereo projection. The formula is r=2ftan⁡(θ/2). The characteristic of this projection method is that it can keep the angle constant, which is a very good property in mathematics, called “Conform”. Keeping the angle constant means that the angle at which any straight line intersects remains the same after the transformation (although the straight line itself may become curved). Under conformal transformation, a circle is still a circle (a straight line can be regarded as a circle with infinite diameter), so to a certain extent, the conformal transformation also keeps the “shape” unchanged. In the following simulation scene, all the boundary lines on the cylindrical wall have all become arcs; the intersection angle of all the lines has also remained unchanged at 90°.

Fisheye lens structure

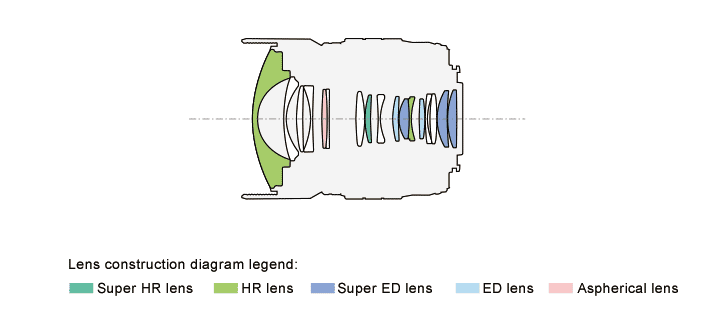
The picture above is a typical fisheye lens structure, the front is a very convex lens group. This lens has 17 lenses, divided into 15 groups, including 1 Aspherical lens, 3 Super ED lenses, 2 ED lenses, 1 Super HR Lens, 2 HR lenses. Of course, fisheye lenses for security cameras generally don’t have so many lens groups, but the overall structure is similar to this.

Installation method of security fisheye camera

According to the previous analysis, security fisheye cameras are generally divided into 360-degree and 180-degree viewing angles according to different lenses. Combining different installation methods and applying to different scenes, they will present different effects.

• Base installation. That is, the camera is placed on a flat base, which is suitable for enclosed small spaces and presents a 180-degree surveillance picture.
• Ceiling installation. Install the camera ceiling in the middle of the ceiling of the room, suitable for a 360-degree fisheye lens, which can monitor the entire room without leaving a dead corner.
• Wall mounted. Use a bracket to fix the camera on a wall on one side of the room, which is suitable for a 180-degree fisheye lens. Of course, a 360-degree fisheye lens can also be installed in this way.

Fisheye lens correction

If we know which projection mapping method is used by the fisheye lens, we can reverse it according to its corresponding principle formula and project it to the plane to correct the image.

Regarding the specific fisheye distortion correction algorithm, it is very professional and has many methods. There are many related patents, academic papers and many researchers on the Internet. The author’s usual work does not involve this area, and there is not enough research on this, and it cannot be carried out in depth. Interested readers can study it by themselves.