Lens of security camera

The optical performance of the lens used by the security camera is basically the same as the lens used by other photographic and camera equipment, so the lens of the security camera also follows the basic optical imaging principle.

Focal length

Focal length, also known as focal length, is a measure of the concentration or divergence of light in an optical system. It refers to the distance from the center of the lens to the focal point of the light.

In a security camera, it is the distance from the optical center of the lens to the imaging plane of the CMOS sensor.

The lens used by the security camera is a convex lens, so the focal length is positive. After a beam of light passes through the convex lens, it will be focused on a point of the CMOS sensor.

Angle of view

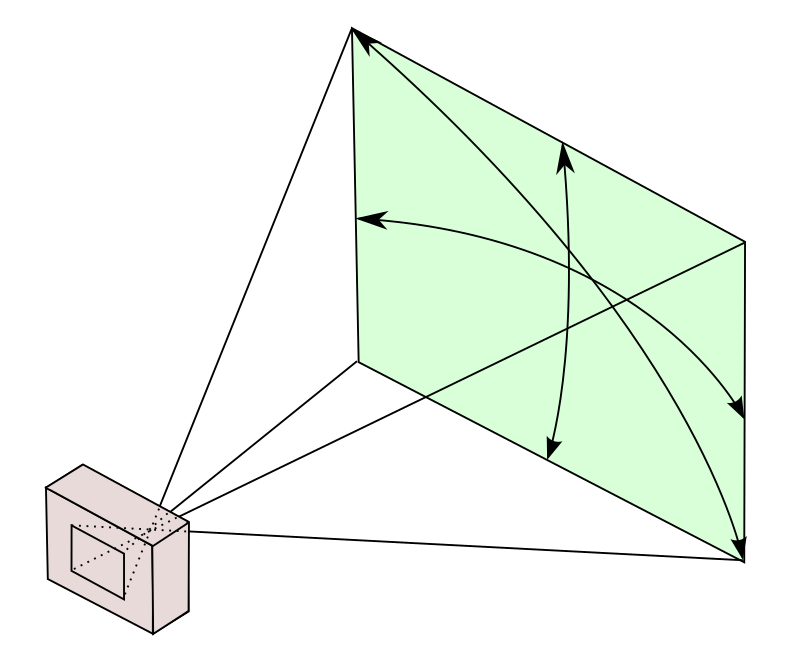
In photography, the angle of view is the range of angles within which the camera can receive images in the general environment, and it can also be often referred to as the field of view.

The angle of view describes the image angle that the camera lens can shoot. Generally speaking, the imaging circle of the lens is large enough to completely cover the photosensitive element sensor (the situation that cannot be covered will be discussed below).

Because the actual shooting target is three-dimensional, the camera’s angle of view can be expressed as a vertical angle of view, a horizontal angle of view, and a diagonal angle of view.

Angle calculation formula

$θ = 2tan^{-1}\dfrac{L}{2f}$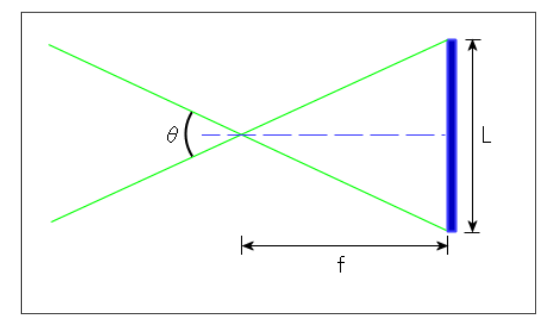

Among them, θ is the angle of view, L is the image sensor size, and f is the focal length. The image sensor has side length, width and length, and diagonal length. The corresponding calculated viewing angles are horizontal viewing angle, vertical viewing angle and diagonal viewing angle.

It can be seen from the above formula that the viewing angle of the camera for a given scheme (that is, the sensor size is determined) is only related to the focal length of the lens. Many times we think it has something to do with the camera resolution, but it has nothing to do with it.

According to the above formula, we will calculate the visible distance of a camera with a 1/3’, 2.8mm lens.

Corresponding to 1/3’sensor-the size of the target surface is width 4.8mm*height 3.6mm, and the diagonal is 6mm. Substituting into the formula, the calculation can be obtained:

$ Horizontal θ = 2tan^{-1}\dfrac{4.8}{2*2.8} =81.2°$

Manufacturers such as Hikvision(HIK Design tool), Axis, and Samsung all provide calculation tools for lens viewing angles, which can be used for reference. Also you can try our Field of camera View.

In actual security projects, in addition to considering the viewing angle of the lens, another viewing distance is more important. For different monitoring purposes, such as seeing the face clearly, seeing the license plate, identifying the gender of men and women, etc., how do we choose a camera, how to choose a suitable camera from the pixel density, you can refer to this article: Camera selection based on pixel density.

According to the formula, we can calculate the viewing angle of cameras with different focal lengths.

LENS surface size	2.8MM	3.6MM	4MM	6MM	8MM
1/1.8′	96.01°	81.65°	75.73°	54.8°	42.49°
1/2.8′	84.87°	70.83°	65.24°	46.21°	35.49°
1/3′	81.2°	67.38°	61.79°	43.6°	33.4°
1/4′	65.47°	53.13°	48.46°	33.4°	25.36°

(Note: The data is for reference only. The lens size is an ideal situation where the camera sensor size is the same. In practice, the camera may not reach the ideal situation, for example, the target surface of the lens is larger than the sensor target surface.)

From the above calculation, we can see that the larger the target surface, the larger the viewing angle. The smaller the focal length, the larger the viewing angle.

Target surface

The concept of the target surface of the lens is the same as the target surface of the sensor, which is the size of the image circle of the lens mentioned above. The size of the sensor is generally expressed by the length of its diagonal, and the target surface of the lens generally refers to its diameter. Like the sensor, the lens target surface is also expressed in inches. Common ones are 1/2’, 1/2.5’, 1/2.7’, 1/3’ and so on.

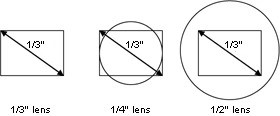
If the target area of the lens cannot cover the entire sensor, the image circle will be seen, and the actual image will be accompanied by severe edge vignetting. In this state, the viewing angle will be limited by the imaging range. (The situation on the left side of the picture below)

On the other hand, if the target surface of the lens is much smaller than the target surface of the sensor, the imaging capability of the sensor will be wasted a lot. (The situation on the right side of the picture below)

So the best case is that the lens target surface and the sensor target surface are exactly the same. Generally, we default to discuss the camera imaging effect in this case. (The situation in the middle of the picture below)

Aperture

Aperture, a component used to control the size of the lens aperture. Through this aperture, the depth of field of the lens can be controlled, and the amount of light (ie exposure) can be controlled in conjunction with the shutter. For a lens that has been manufactured, the diameter of the lens cannot be changed at will, but a polygonal or circular hole grating with a variable area can be added to the lens to control the amount of light passing through the lens. This device is called an aperture.

In optics, the aperture is also called the focal ratio (f-number, or f-number, f-ratio, relative aperture, aperture value, aperture coefficient, etc., habitually referred to as “aperture”) to express the relationship between the focal length of the lens and the diameter of the aperture . Simply put, the focal ratio is equal to the number of focal lengths divided by the number of apertures.

ƒ value formula: D = ƒ/N

In the above formula, ƒ is the focal length, N is the digital representation of the actual aperture, and D is the aperture value.

Conventionally, “ƒ/#” is regarded as a whole to describe the aperture value, and the value replaces the # in the symbol when writing. For example, if the focal length value is 1 times the aperture diameter, then the ƒ value is ƒ/1.0, or N=1.

From the formula, we can see that the illuminance of the light passing through the lens to the photosensitive element sensor is proportional to the square of the aperture aperture, and inversely proportional to the square of the aperture number.

The smaller the f-number, the larger the aperture, the greater the amount of light, and the shallower the depth of field (see article depth of field).

Ƒ/#

0.5

0.7

1.0

1.4

2

2.8

4

5.6

8

11

16

The square ratio of the two adjacent aperture numbers in the full-level aperture value is 1:2, so the illuminance of the lens of the adjacent two aperture values is doubled.

In addition to the aperture size, the amount of light can be controlled by controlling the exposure time of the lens. At the same time, some automatic gain methods (ie exposure control) can be added. In special scenes, such as strong contrast between light and dark, clear image effects can be obtained. Such as BLC, WDR, exposure area. There will be articles about exposure control, WDR wide dynamic and so on in the future.

Depth of field

There is a permissible circle of confusion before and after the focal point. The distance between these two circles of confusion is called the depth of field, that is: before and after the subject (focus point), the image still has a clear range, and this clear range is Depth of field. In other words, the front and back depth of the subject and the degree of blurring of the image presented on the screen are all within the limit of the permissible circle of confusion.
Generally,

1. The larger the aperture, the smaller the depth of field; the smaller the aperture, the greater the depth of field;
2. The longer the focal length of the lens, the smaller the depth of field; the shorter the focal length, the greater the depth of field;
3. The farther the distance, the greater the depth of field; the closer the distance, the smaller the depth of field.

For more about the concept of depth of field, you can refer to this article: Depth of Field.

Lens interface

In the security industry, there are mainly the following types of commonly used lens interfaces:

M12/D14 interface
Such lenses are generally called trigger lenses, or MTV lenses. Among them, the M12 lens interface is threaded, and the D14 is in-line. The complete description of the M12 interface is generally M12P0.5, which means that the nominal diameter of the lens interface thread is 12mm, and P0.5 means that the thread pitch is 0.5mm. Similarly, D14 means that the diameter of the lens interface is 14mm.

Because M12/D14 are relatively small interfaces, sometimes these two interfaces are called S interfaces.

C/CS interface
C refers to cinema, and the C-mount lens originated from the camera lens. At present, the C interface is a standard interface for security cameras, machine vision cameras, microscopes, etc.
The C-mount lens provides a male port thread to match the camera’s female port. According to the “ANSI B1.1” standard design, the diameter of the thread is 1 inch (25 mm), with 32 threads per inch. The distance from the C-mount lens to the chip sensor is 17.526 mm.

The C interface is the original standard, and the CS interface is an upgrade to it, which can reduce manufacturing costs and reduce the size of the sensor. Most security cameras and lenses sold on the market now use the CS interface standard.

The distance between the CS interface lens and the chip sensor is 12.52 mm, and the other parameters are the same as the C interface. So we can use a “5mm mount” to convert the “C mount lens” into a “CS mount” lens.

If the camera cannot focus, you can consider whether the wrong lens interface type is used, and whether a 5mm adapter ring needs to be added.

Bayonet
For professional photography and video cameras, the lens interface generally used is bayonet type. Commonly have A bayonet, E bayonet, EF bayonet, K bayonet, Q bayonet, 645 bayonet, etc.

Large diameter interface
For machine vision and industrial cameras, because the sensor target size used is large, lenses with a large interface diameter, such as M42 and M58, are used, so the corresponding lens interface diameters are 42mm and 58mm.

Lens classification

We can classify the lenses through the relevant parameter information of the above lenses.

By focal length
Fixed focal length lens (medium, long and short focal length lens)
Variable focal length lens

By focusing method
The zoom lens can be divided into manual focus and electric automatic zoom

By the aperture
According to the aperture, it can be divided into fixed aperture and variable aperture.
Variable aperture can be divided into manual aperture and automatic aperture.
Automatic iris lens has video drive, DC drive, P-iris, i-CS and other types.

By installation interface
According to the type of lens interface, you can refer to the above introduction.

According to the use environment
It can be divided into starlight lens, day and night lens, fog lens and so on.

Special purpose lenses and functions

• Fisheye lens (many parameter performance of fisheye lens does not follow the general lens rules, a follow-up article will introduce it separately)
• Fog lens
• Anti-shake (Eis)
• Distortion correction
• In addition to heat waves
• Starlight lens
• Near infrared
• The camera supports automatic back focus adjustment (ABF)

Lens lens material

The general security lens lens material is plastic or glass, and more is a mixture of the two. Because a lens may have more than one lens. For example, a certain security lens indicates that the lens composition is 2G5P, which means that it has 7 layers of lenses, including 2 layers of glass and 5 layers of plastic.

The advantages of plastic lenses are lighter weight, cheaper price, and easier casting and film forming of aspheric surfaces. The disadvantage is that the refractive index is lower, the surface is easier to scratch than glass, and the surface shape is not as accurate as glass.

Lens evaluation

The lens evaluation function is not linear, and commonly used lens evaluation optimization methods include constrained least squares algorithm and comprehensive optimization method. The content of the evaluation includes color, field of view balance, distortion, etc.

Other parameters for evaluating lens performance include:

• MTF, Modulation Transfer Function (modulation transfer function) is a more scientific method to analyze the effect of the resolution of the lens. Although MTF is a standard, some image effects can be measured without standardization, so MTF is just a reference value and not all.
• Transmittance (light transmittance). Light transmittance is a physical term, which means the ability of light to pass through a medium, and is the percentage of the luminous flux through the lens to its incident luminous flux. The lens of the lens is not 100% light-transmissive, there will be reflection, scattering, refraction, and diffraction. Generally, coating the lens of the lens can reduce these factors and increase the light transmittance of the lens. The best lens at present can achieve a light transmittance of 99.9%.
• Resolution (lens resolution). The resolution of a lens is the ability to distinguish the density of black and white stripes. The highest density that the lens can distinguish is the limit resolution of the lens, in units of line pairs per millimeter (lp/mm). The general resolution at the edge of the lens is equal to 60% of the center resolution. The resolution of the lens is best matched with the resolution of the sensor.
• Chromatic aberration, aberration, diffraction. For example, the micron-order diffraction grating laminated structure developed by Canon uses reverse thinking to control the optical path by using diffraction phenomena that usually degrade image quality. One DO lens can achieve the compensation effect of fluorite lens and aspherical lens. The use of DO lenses can compensate for chromatic aberrations and achieve high image quality and miniaturization of the lens.